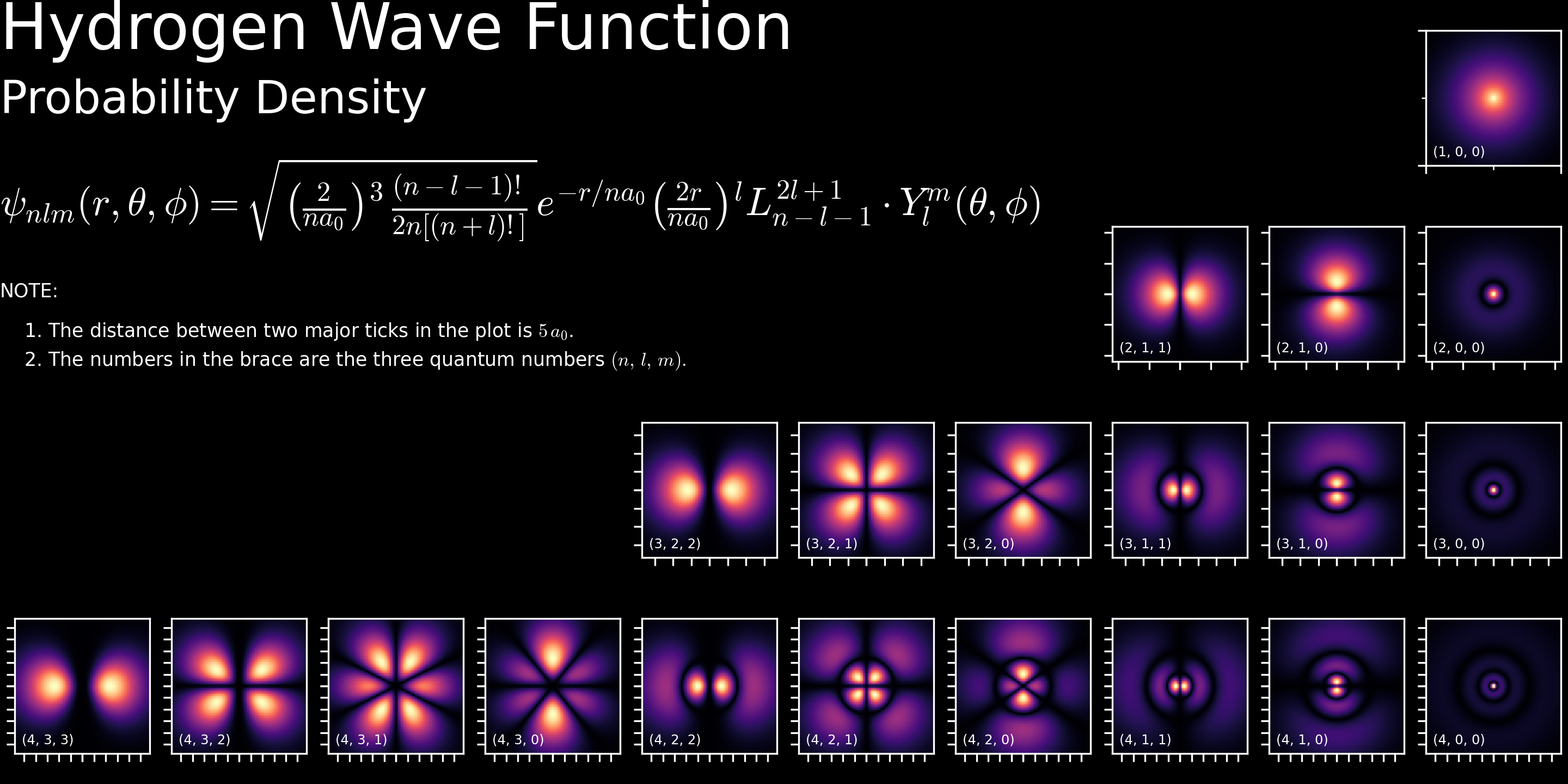
Hydrogen Wave Function
The normalized hydrogen wave function1
\[\begin{equation} \label{eq:hydro_wfc} \psi_{nlm}(r,\theta,\phi) = \sqrt{ \left(\frac{2}{na_0}\right)^3\, \frac{(n-l-1)!}{2n[(n+l)!]} } e^{-r / na_0} \left(\frac{2r}{na_0}\right)^l L_{n-l-1}^{2l+1} \cdot Y_l^m(\theta, \phi) \end{equation}\]Codes
Below is the
code
that generates the above figure, where the analytic hydrogen
wave function was obtained from sympy.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
#!/usr/bin/env python
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.ticker import AutoMinorLocator
from sympy import lambdify, integrate, oo
from sympy.abc import r, theta, phi
from sympy.physics.hydrogen import R_nl, Psi_nlm
plt.style.use('dark_background')
mpl.rcParams['mathtext.fontset'] = 'cm'
def cart2sphe(x, y, z):
'''
3D Cartesian coordinates to spherical coordinates.
input:
x, y, z : numpy arrays
'''
xy2 = x**2 + y**2
r = np.sqrt(xy2 + z**2)
theta = np.arctan2(np.sqrt(xy2), z) # the polar angle in radian angles
phi = np.arctan2(y, x) # the azimuth angle in radian angles
phi[phi < 0] += np.pi * 2 # np.arctan2 returns the angle in the range [-pi, pi]
return r, theta, phi
################################################################################
if __name__ == "__main__":
Nmax = 4
nlms = [
(n, l, m)
for n in range(1, Nmax+1)
for l in range(n)
for m in range(l+1)
]
PSI = [
lambdify((r, phi, theta), Psi_nlm(n, l, m, r, phi, theta), 'numpy')
for n, l, m in nlms
]
################################################################################
# print(plt.figaspect(2 / Nmax),)
fig = plt.figure(
figsize=(9.6, 4.8),
# figsize=plt.figaspect(2 / Nmax),
dpi=300,
constrained_layout=True
)
axes_array = np.zeros((Nmax, (Nmax*(Nmax+1))//2), dtype=int)
axes_id = 0
for ii in range(Nmax):
lm_sum = ((ii+1) * (ii+2)) // 2
for jj in range(0, lm_sum):
axes_id += 1
axes_array[ii, -(jj+1)] = axes_id
axes = fig.subplot_mosaic(
axes_array,
empty_sentinel=0,
)
axes = [axes[ii+1] for ii in range(len(axes))]
cut_planes = np.ones(len(axes), dtype=int) * 2
################################################################################
for ii in range(len(axes)):
n, l, m = nlms[ii]
# L = np.ceil(integrate(R_nl(n, l, r, Z=1)**2 * r**3, (r, 0, oo)) / 10) * 10
# L = integrate(R_nl(n, l, r, Z=1)**2 * r**3, (r, 0, oo)) * 2
# N = 100
# print(n, l, L)
if n == 1:
L, N = 1.5*n**2 + 1.0, 100
else:
L, N = 1.5*n**2 + 5.0, 100
a0, b0 = np.mgrid[
-L:L:N*1j,
-L:L:N*1j
]
nx, ny = a0.shape
xyz_planes_sphe = [
cart2sphe(a0, b0, 0),
cart2sphe(0, a0, b0),
cart2sphe(a0, 0, b0),
]
ax = axes[ii]
ax.set_aspect(1.0)
r0, theta, phi = xyz_planes_sphe[cut_planes[ii]]
wfc = PSI[ii](r0, phi, theta).reshape(nx, ny)
ax.pcolormesh(a0, b0, np.abs(wfc), cmap='magma')
ax.set_xlim(-L, L)
ax.set_ylim(-L, L)
STEP = 5
if n == 1:
ax.set_xticks([-2.5, 2.5])
ax.set_yticks([-2.5, 2.5])
ax.xaxis.set_minor_locator(AutoMinorLocator(n=2))
ax.yaxis.set_minor_locator(AutoMinorLocator(n=2))
else:
ax.set_xticks([-x for x in np.arange(0, L, STEP)] + [x for x in np.arange(0, L, STEP)])
ax.set_yticks([-x for x in np.arange(0, L, STEP)] + [x for x in np.arange(0, L, STEP)])
ax.set_xticklabels([])
ax.set_yticklabels([])
ax.text(0.05, 0.05, "({}, {}, {})".format(n, l, m),
fontsize='xx-small',
ha='left', va='bottom', transform=ax.transAxes, color='w')
fig.text(0.0, 1.00, r'Hydrogen Wave Function',
fontsize=28,
ha='left', va='top', transform=fig.transFigure, color='w')
fig.text(0.0, 0.90, r'Probability Density',
fontsize=20,
ha='left', va='top', transform=fig.transFigure, color='w')
fig.text(0.0, 0.80, r'$ \psi_{nlm}(r,\theta,\phi) = \sqrt{ \left(\frac{2}{na_0}\right)^3\, \frac{(n-l-1)!}{2n[(n+l)!]} } e^{-r / na_0} \left(\frac{2r}{na_0}\right)^l L_{n-l-1}^{2l+1}\cdot Y_l^m(\theta, \phi)$',
fontsize='xx-large',
ha='left', va='top', transform=fig.transFigure, color='w')
# fig.text(0.00, 0.64, "NOTE:\n\t1. The distance between two major ticks in the plot is $5\,a_0$,\n\t2. The number in the braces are the three quantum numbers $(n, l, m)$",
# fontsize='small',
# linespacing=1.8,
# ha='left', va='top', transform=fig.transFigure, color='w')
fig.text(0.00, 0.64, "NOTE:",
fontsize='small',
ha='left', va='top', transform=fig.transFigure, color='w')
fig.text(0.00, 0.59, " 1. The distance between two major ticks in the plot is $5\,a_0$.\n 2. The numbers in the brace are the three quantum numbers $(n,\,l,\,m).$",
fontsize='small',
linespacing=1.5,
ha='left', va='top', transform=fig.transFigure, color='w')
plt.savefig('hydro_wfc.png')
# from subprocess import call
# call('feh -xdF hydro_wfc.png'.split())